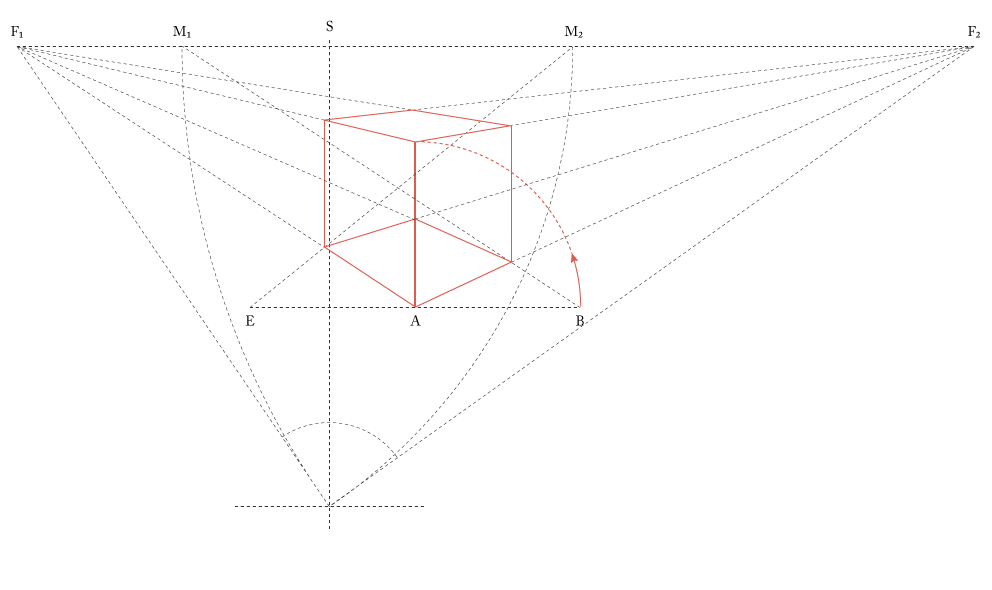
Messpunkt-Methode
Die Messpunkt-Methode behilft sich bei der perspektivischen Darstellung mit zwei Messpunkten, die die Lage eines Objektes im Raum definieren. Sie ist die einfachste der drei gezeigten Varianten, wenn es darum geht, einen Würfel perspektivisch zu konstruieren. Die Einfachheit bezieht sich auf die wenigen Linien, die zur fertigen Zeichnung benötigt werden. Im Hinblick auf eine schnelle Freihandskizze ist sie jedoch wegen der Fluchtpunkte und Kreisbogen zu unhandlich, hier wäre die Neue Methode klar im Vorteil.
Auch ist eine Konstruktion mittels Messpunkte nicht sehr verständlich, was bereits George Adolphus Storey bemängelte, aus dessen „Theory and Practice of Perspective“ ich die Anwendung entnommen habe, hier nur unter dem Namen Messpunkt-Methode vorgestellt.
Räumliche Darstellung eines Würfels
Horizontlinie
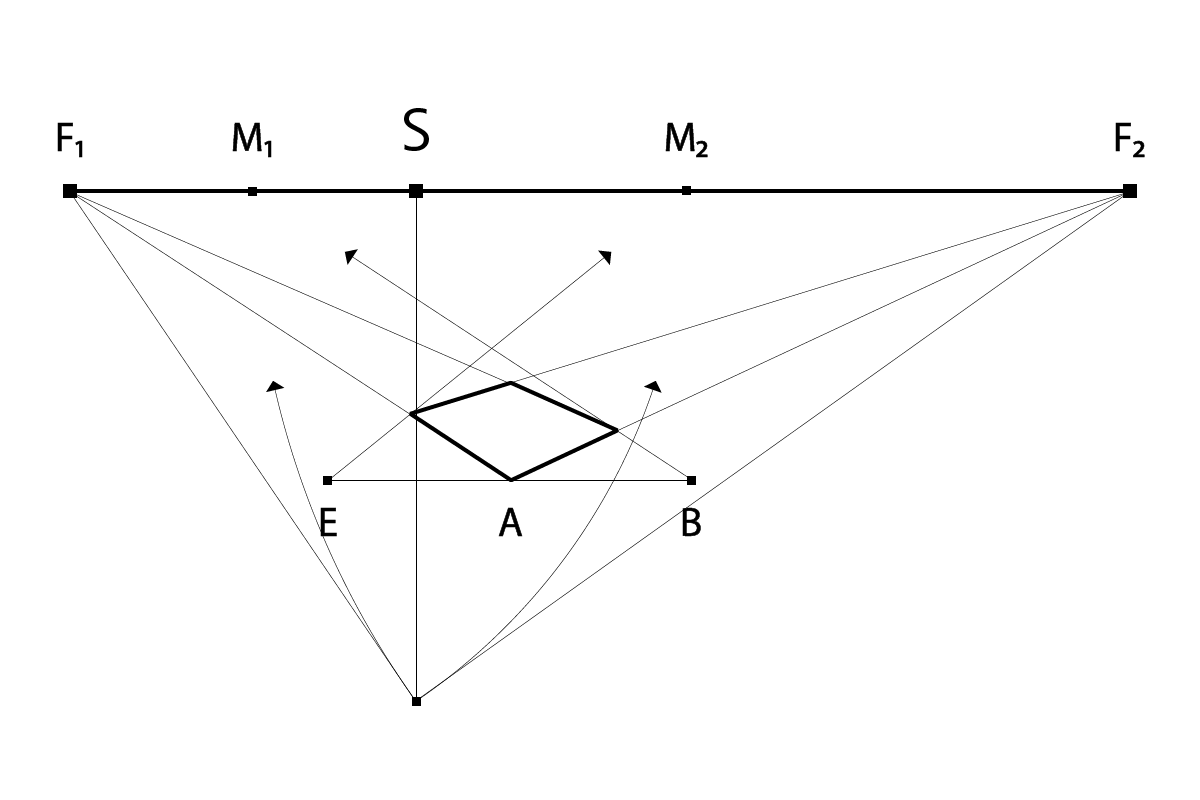
Als erstes wird auf der Horizontlinie Punkt S, der Sichtpunkt, festgelegt. Die Lage des Betrachters gilt es nun als nächstes zu bestimmen. Dieser liegt in einer Linie mit dem Sichtpunkt und in einem rechten Winkel zu den beiden Fluchtpunkten. Man kann daher die Zeichnung auch von diesem Winkel aus beginnen, indem man zuerst die beiden Nebenwinkel bestimmt, die zusammen 90° ergeben sollen, damit sich die drei Winkel zu 180° ergänzen. In diesem Beispiel sind es 56° und 34°.
Vom vorderen Winkel aus (Lage des Betrachters) werden Linien zu den Fluchtpunkten gezogen. Diese sind die Radien für die Übertragung der beiden Messpunkte auf die Horizontlinie, Zentren der Radien sind F₁ bzw. F₂.
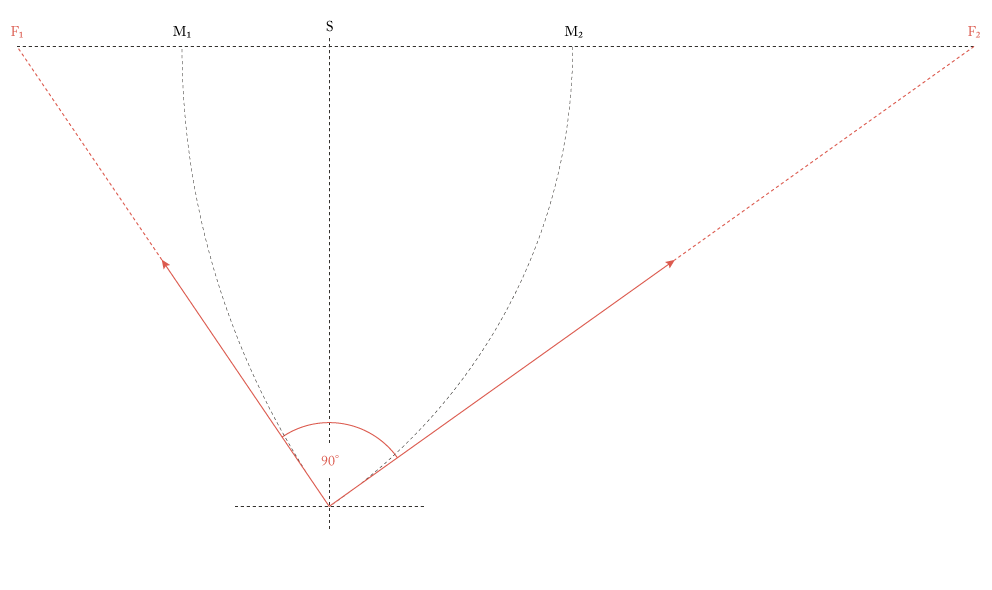
Objektlinie
Die Objektlinie mit Punkt A (vordere Kante des Würfels) wird eingezeichnet und die Strecken AF₁ und AF₂ gezogen, die so genannten Fluchtlinien. Die Kantenlänge des Würfels wird durch die Strecke AB festgelegt und auf die andere Seite übertragen, daher AB = AE. Nun wird EM₂ und BM₁ gezeichnet, deren Schnittpunkte mit den Fluchtlinien ergeben die perspektivischen Längen der Würfelseiten.
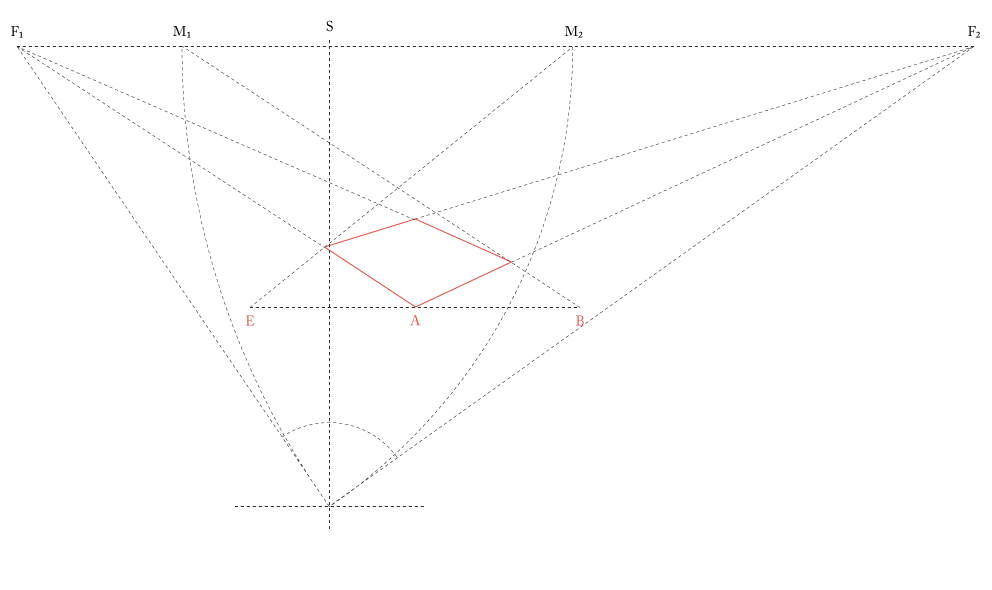
Objekthöhe
Die Strecke AB ist die Höhe des Würfels. Die Fluchtlinien werden gezogen und die Konstruktion entsprechend ihren Schnittpunkten ergänzt.