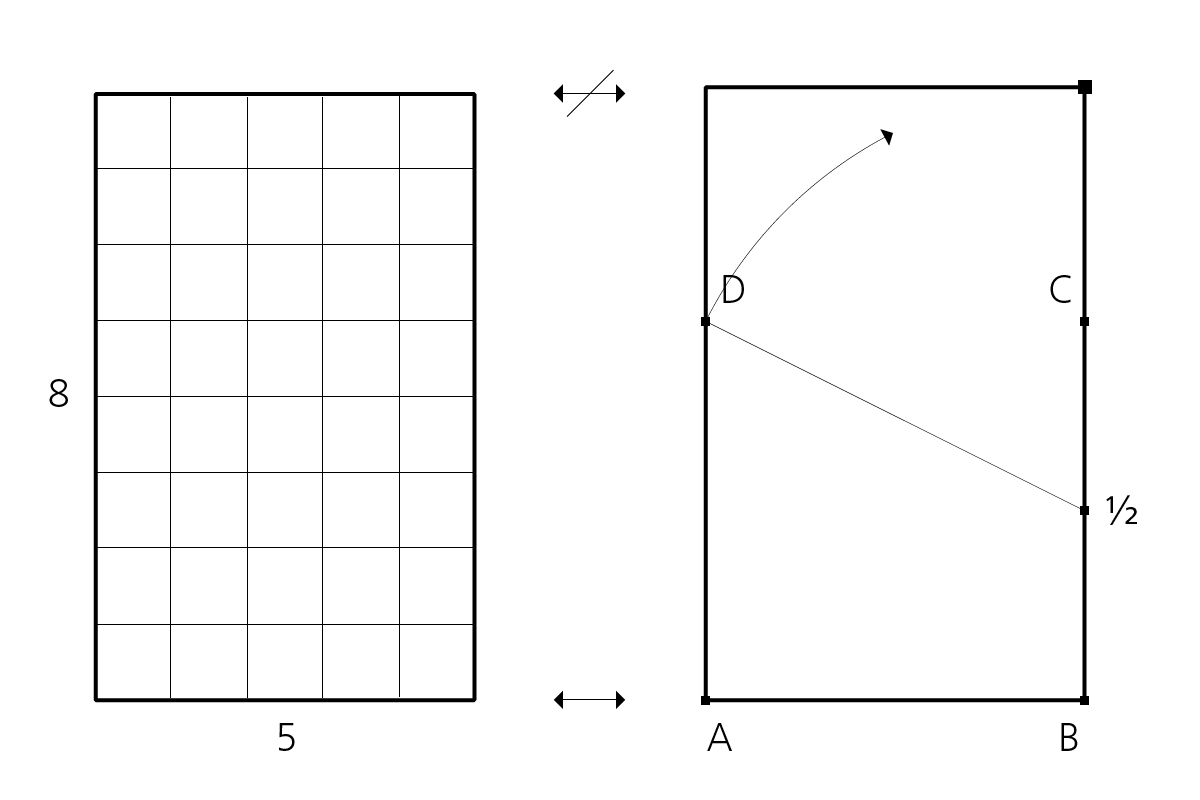
5:8 oder 1:1,618

Ein Goldenes Rechteck ist ein Rechteck mit den Seitenlängen im Verhältnis des Goldenen Schnitts, gerundet auf 1:1,618. Zur einfacheren Handhabung und technischen Zwecken findet das Rechteck im Seitenverhältnis von 5 zu 8 Anwendung, dessen Quotient 1:1,6 beträgt.

Die geometrische Konstruktion eines Goldenen Rechtecks ist dem Auron der Orthogonreihe des Wolfgang von Wersin identisch. Sie erfolgt, ausgehend von einem Quadrat ABCD, durch Schwenkung der Halbdiagonalen.

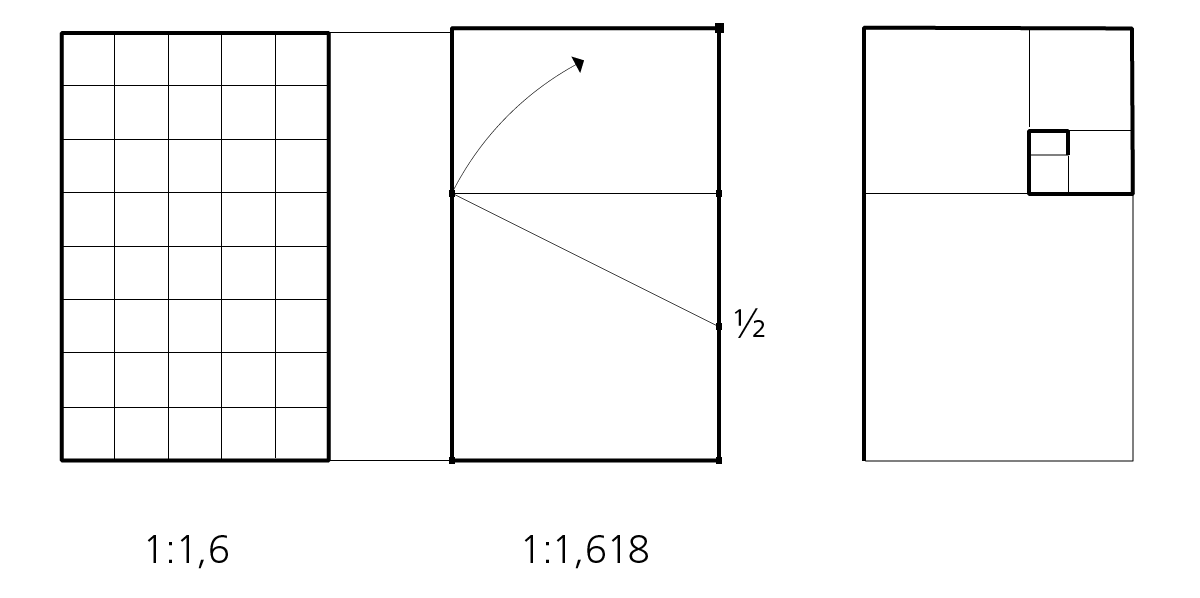
Das Verhältnis zwischen Quadrat, √5-Rechteck und Goldenem Rechteck ist in der Dynamischen Symmetrie von Jay Hambidge von Bedeutung und hier genauer dargestellt. Hambidge nennt das Goldene Rechteck Rectangle of the Whirling Squares: wird ein Quadrat von dessen Fläche abgezogen, entsteht ein Goldenes Rechteck, zieht man wieder ein Quadrat ab, entsteht ein weiteres. In spiralförmiger Anordnung verläuft dieses System weiter.