Wurzelzahlen-Folge
Irrational und dynamisch
In der Gestaltung werden Rechtecke einer verhältnismäßigen Abfolge gerne mit der Bezeichnung Wurzelzahlen-Folge oder Wurzel-Rechtecke benannt.
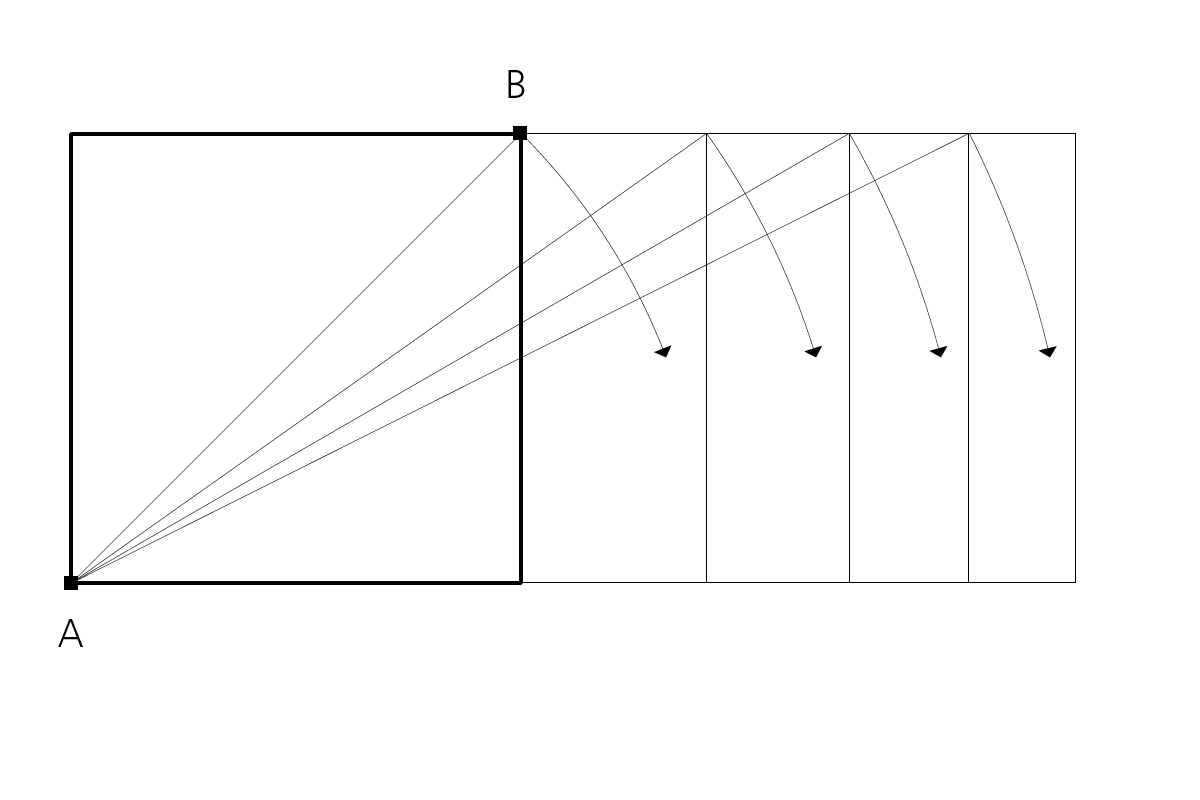
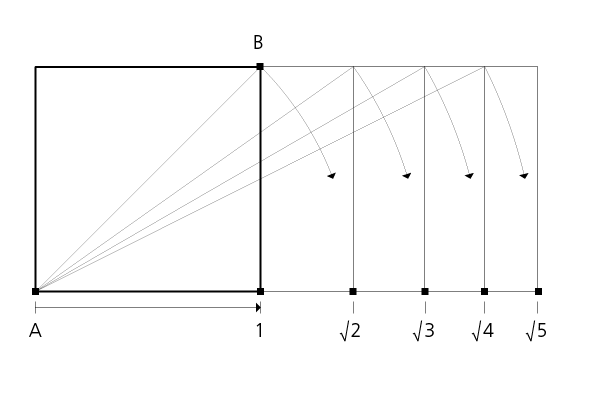
Wurzel-Rechtecke werden über die Diagonale des vorangegangenen Rechtecks konstruiert. Ausgehend von einem Quadrat mit der Seitenlänge 1 entsprechen die folgenden Seitenlängen der Rechtecke den Werten von √2, √3, √4 usw., wodurch die Benennung als Wurzelzahlen-Folge ersichtlich wird.
Innerhalb der Dynamischen Symmetrie von Jay Hambidge sind sie die zentralen Elemente.
Das √5-Rechteck ist dabei in doppelter Hinsicht von Bedeutung, da es auch über ein Goldenes Rechteck plus sein Reziprok erzeugt werden kann.
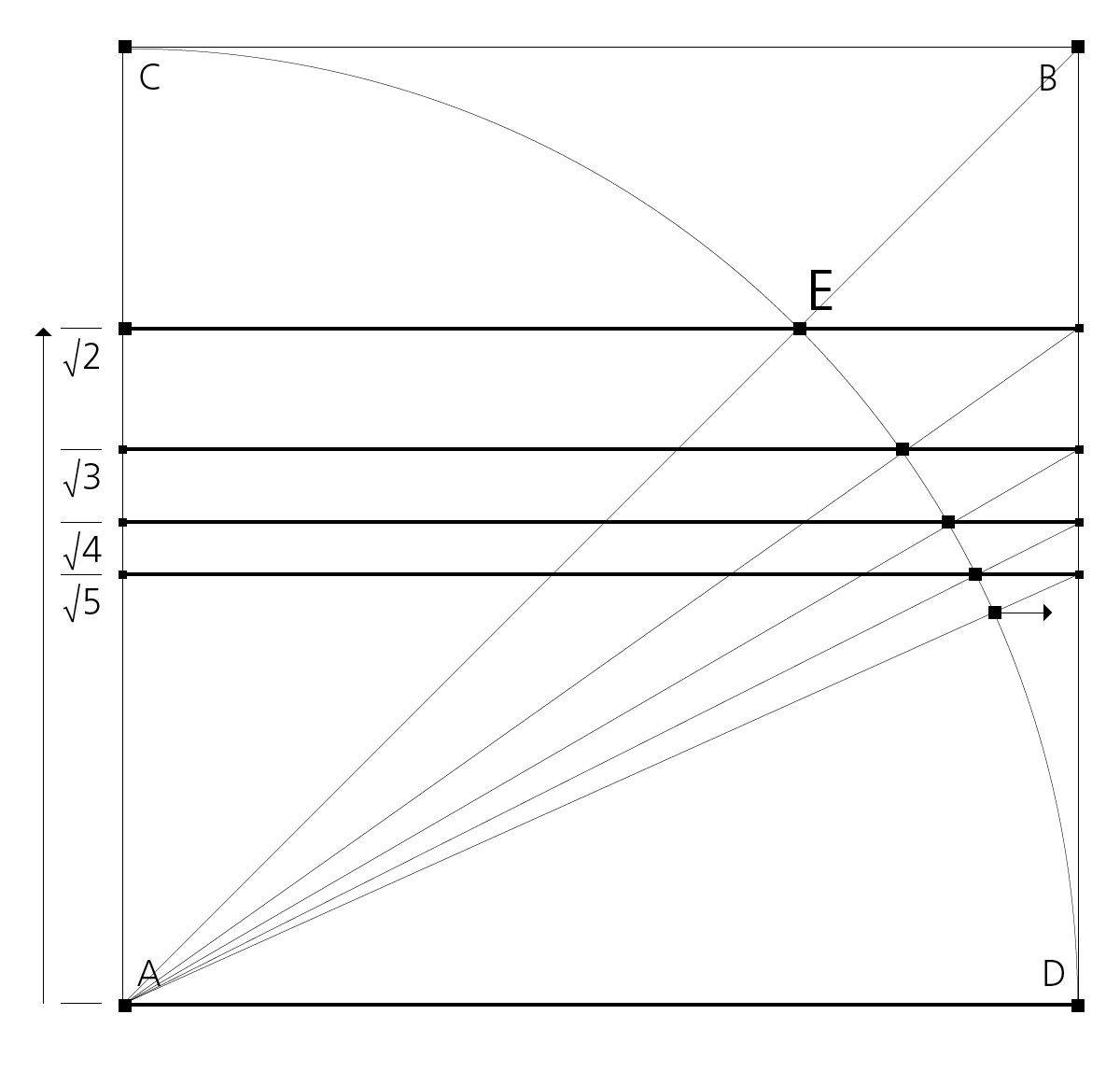
Konstruktion im Quadrat
Diagonale AB und Kreisbogen CD um Punkt A definieren den Schnittpunkt E. Eine horizontale Linie durch Punkt E ergibt ein √2-Rechteck innerhalb eines Quadrats. Dessen Diagonale liefert auf dem Kreisbogen CD den nächsten Schnittpunkt für ein √3-Rechteck, usw.
√5-Rechteck, Quadrat und Goldene Rechteck
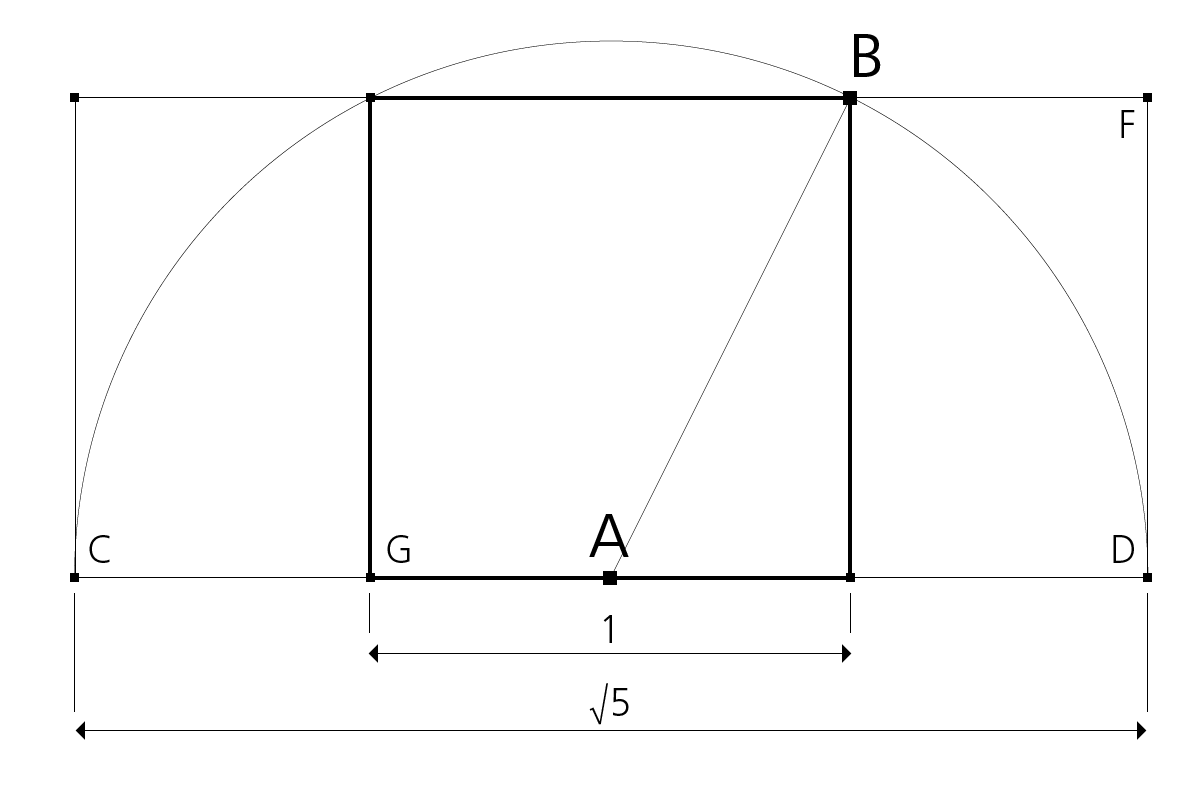
Die Halbdiagonale AB des Quadrats ist der Radius des Halbkreises CD. CF ist ein √5-Rechteck, GF ein Goldenes Rechteck.
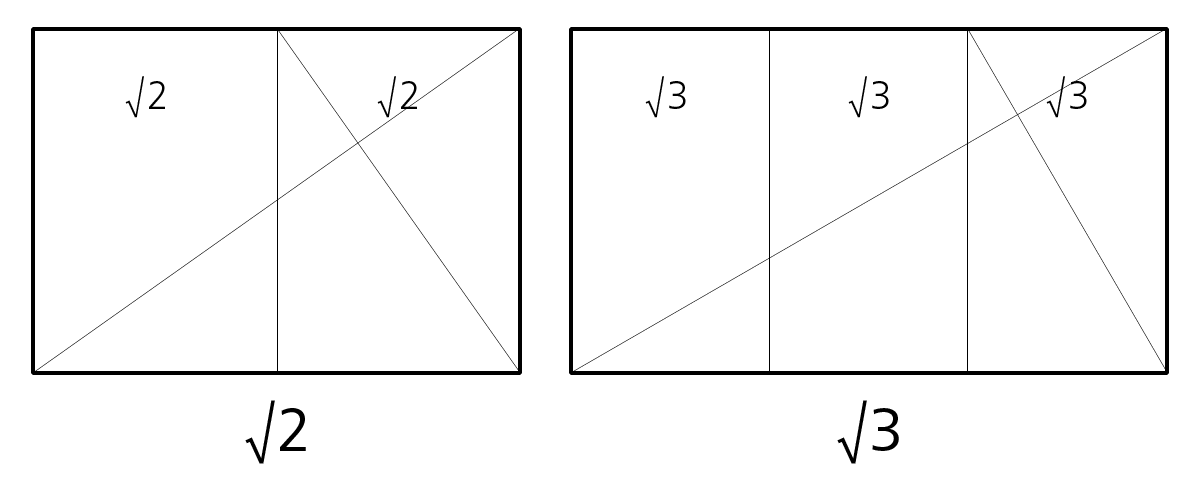
Flächenteilung
Eine Besonderheit der Wurzel-Rechteckfolge ist, dass sich das √2-Rechteck durch seine Reziproke in zwei √2-Rechtecke teilt, das √3-Rechteck in drei √3-Rechtecke usw. Eine gestalterische Abfolge ist somit ersichtlich, welche die Dynamische Symmetrie fordert, um Teilungen und Ergänzungen im selben Maß zu erzeugen.