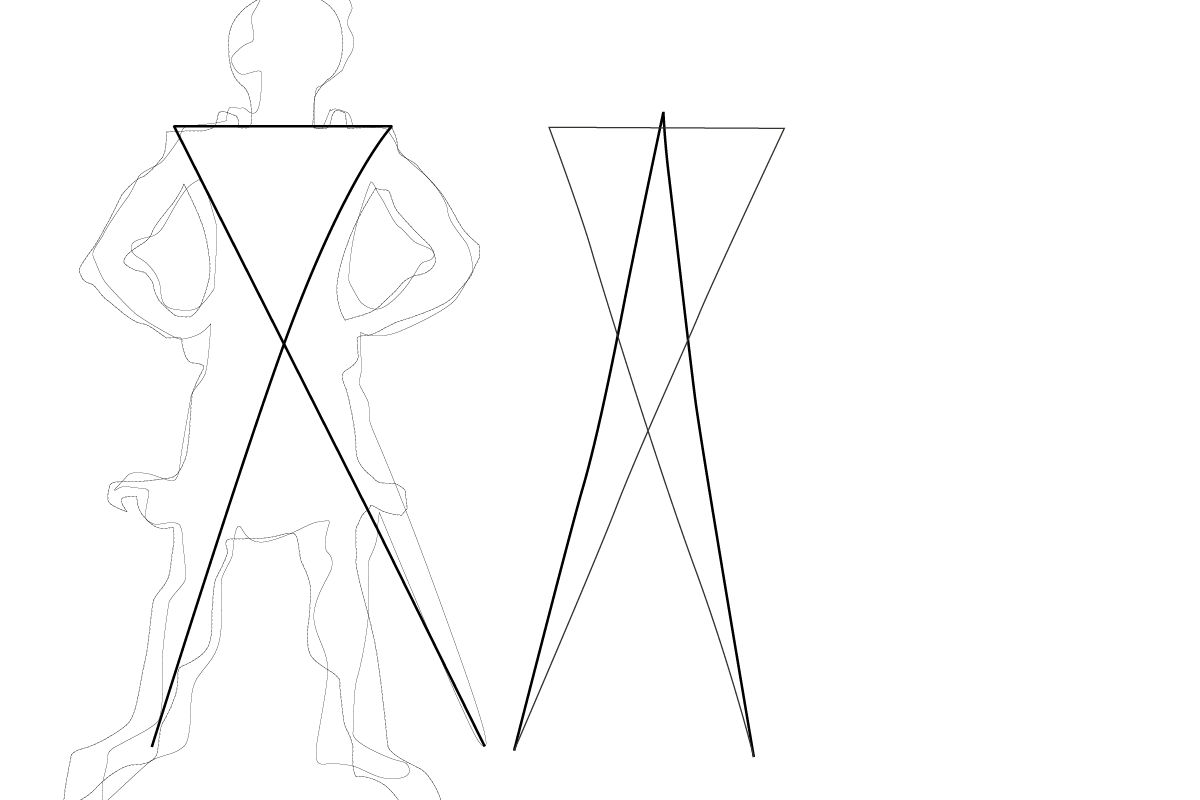
Die Zeichnungen des Villard de Hounnecourt und die Teilung mittels Diagonale

Die Villardsche Figur (auch Villardsches Diagramm genannt) ist eine Methode der geometrischen Teilung von Strecken. Benannt ist die Technik nach Villard de Honnecourt, einem Zeichner aus dem 13. Jahrhundert, dessen Manuskript noch heute in der Pariser Nationalbibliothek erhalten ist.
Die Methode bietet die Möglichkeit, beliebig viele gleich lange Teilstrecken zu definieren, und dies ohne Einzelmessung. So können auch ohne die Skala eines Lineals exakte Teilungen erzeugt werden, die – wie sich noch zeigen wird – besonders diejenigen Teilungen definieren, die harmonisch miteinander in Verbindung stehen.

Eine Einführung in die geometrische Analyse des Villardschen Diagramms gibt Hans Kayser im Heft „Ein harmonikaler Teilungskanon“ von 1946. Hans Kayser, dessen Arbeit die Beziehungen zwischen der Musik mit ihren Harmonie-Regeln und der Zeichnung bzw. den architektonischen Bauten untersucht, beschreibt die Teilungsmethode.

Er überträgt Villards Skizzen von menschlichen Figuren, denen sich kreuzende Linien eingezeichnet sind, auf Rechteckformen. Ein geometrisches Schema wird ersichtlich, denn die Teilung mittels der Diagonale ergibt eine Abfolge in 1/2, 1/3, 1/4, …

Hans Kayser sieht darin die Grundlage zu einer „sukzessiven harmonischen Teilung in pythagoreischer Tradition“, da sich diese Verhältnisfolge auch auf die Einteilung eines Monochords übertragen ließe, welches früher (Antike) gerne zur Verdeutlichung harmonischer Theorien benutzt wurde und in seiner Bedeutung mit dem Namen „Kanon“ identisch war.

Übertragung der Figur auf ein beliebiges Rechteck

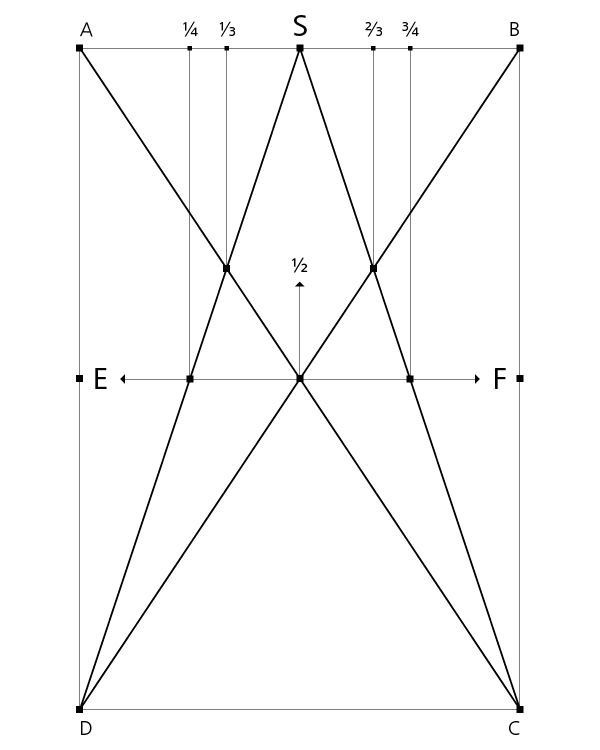
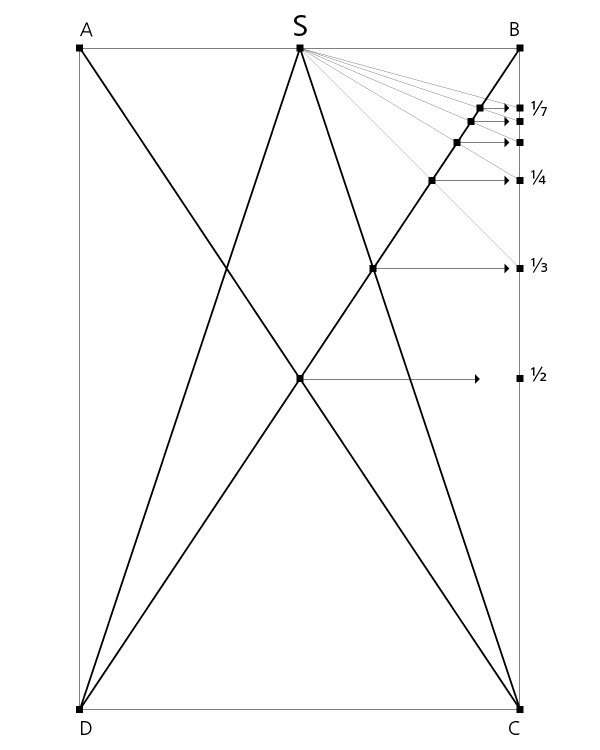
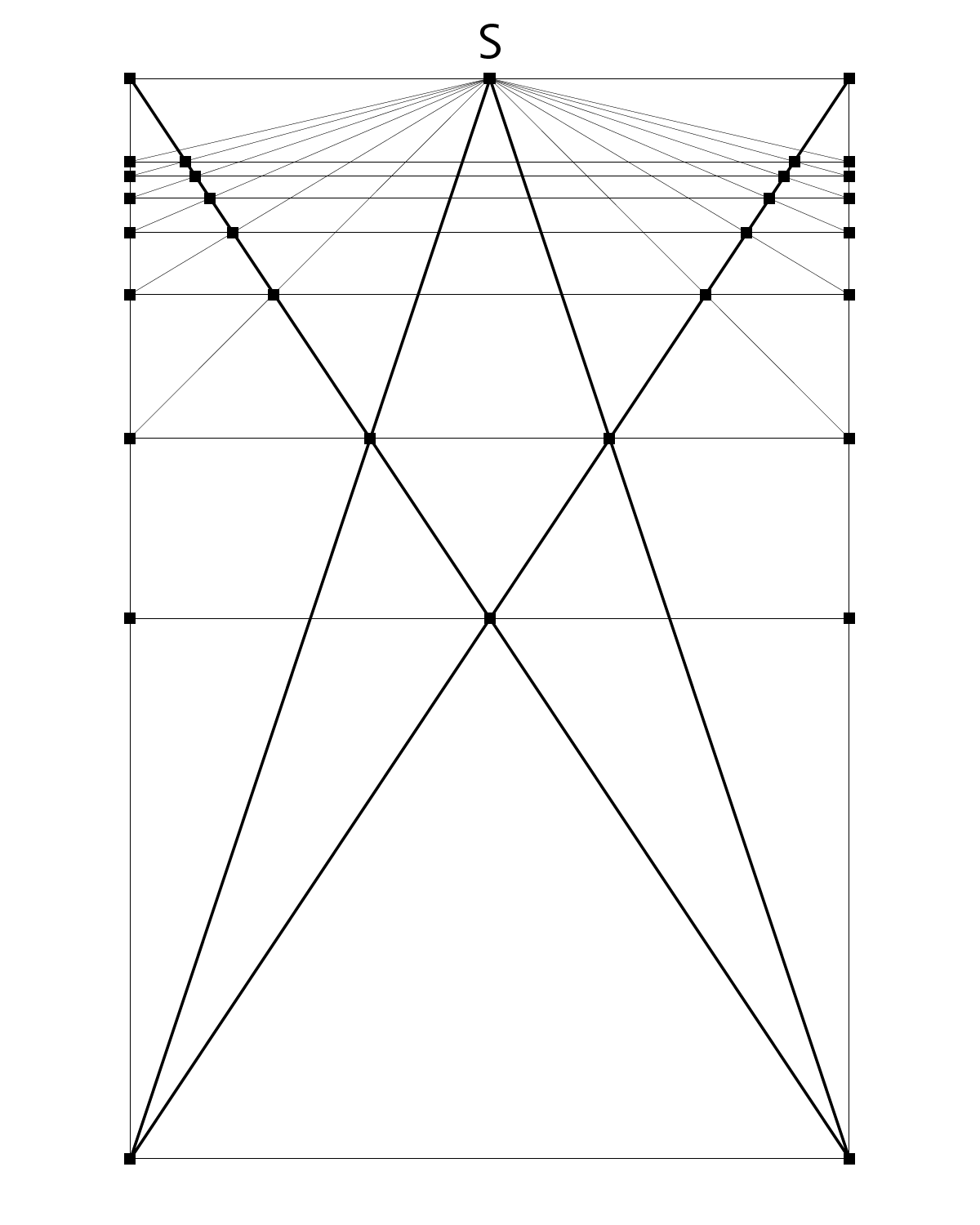
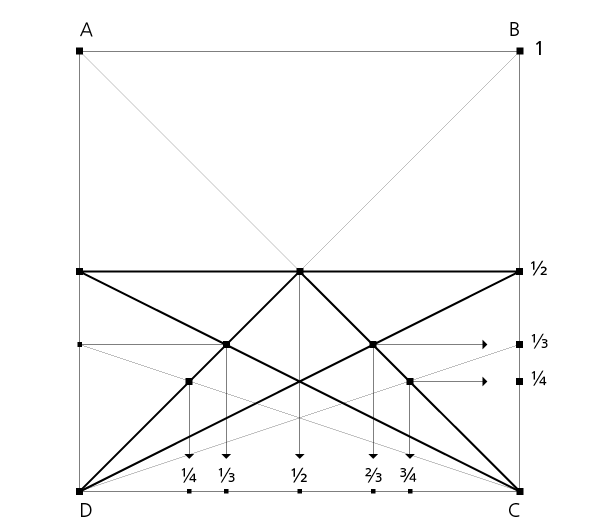
Die Diagonalen des Rechtecks ABCD teilen die obere Strecke AB in Punkt S. Mit den Halbdiagonalen DS und CS ergibt sich die Villardsche Figur in ihrer Grundkonstruktion.

Zur weiteren Abstufung (1/4) werden die Strecken ES und FS gezogen, welche die Diagonalen schneiden, so dass durch die Schnittpunkte eine horizontale Linie gezogen werden kann.

Konstruktion im Quadrat

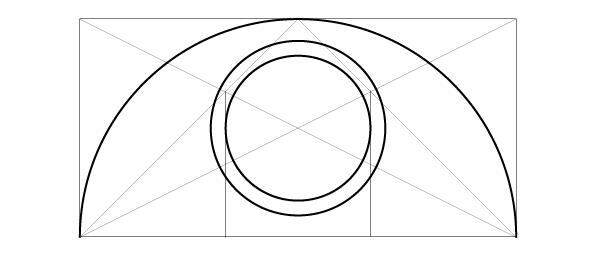
Villardsche Figur in der Architektur

Sebastiano Serlio zeichnete 1545 im „Libro Primo – primi principij della Geometria“ die Villardsche Figur in Rechtecke ein, um Möglichkeiten einer harmonischen Proportion für die Architektur darzustellen, wie hier in einem Doppelquadrat.

Villardsche Figur in der Typographie

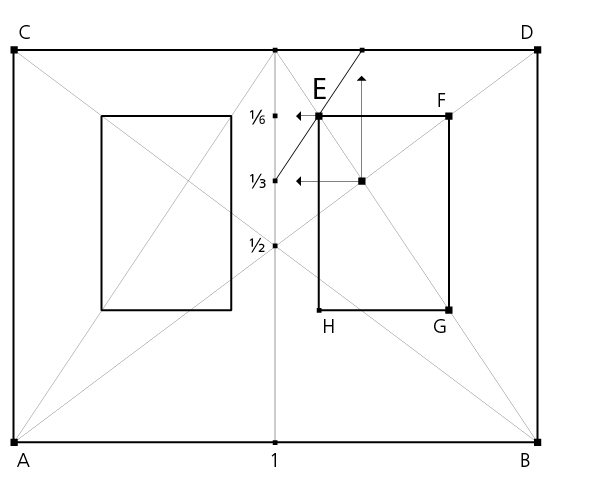
Die Aufteilung einer Buchseite in Ränder und Textfläche lässt sich sehr gut durch geometrische Konstruktion erzeugen. Um hierbei ein harmonisches Verhältnis zu finden, wie etwa im Goldenen Kanon von Jan Tschichold, teilt man die Druckseite mit Hilfe der Villardschen Figur.

Eine Neunteilung, so von J. van de Graaf hergeleitet, nutzte Jan Tschichold für seinen Kanon der Buchseiteneinteilung. Aber auch andere Verhältnisse sind in der Typographie üblich, wie etwa eine Sechsteilung, Tschicholds Nachkonstruktion eines Gebetbuchs aus dem 15. Jahrhundert: