„Wieviele Kaninchenpaare entstehen im Verlauf eines Jahres aus einem Paar?“

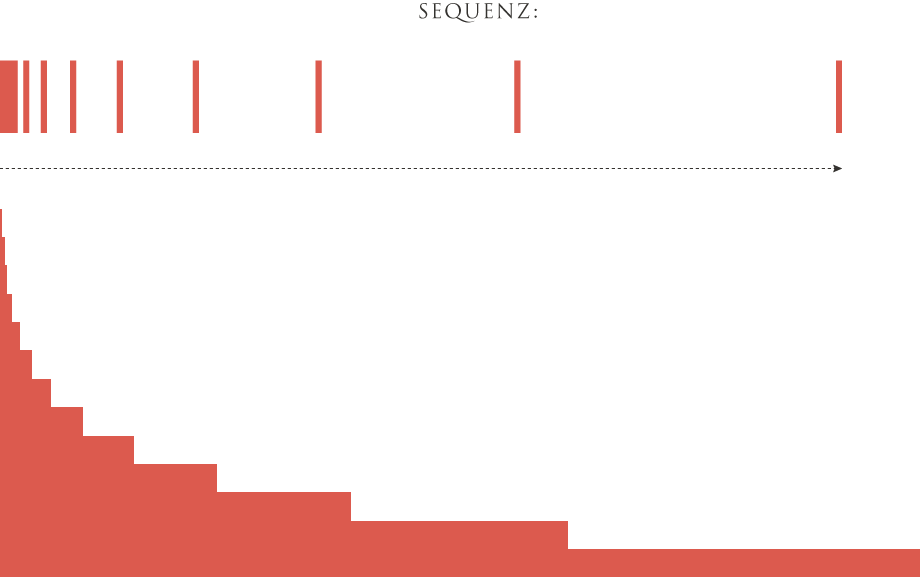
Im Liber abbaci von 1228, einem Arithmetik-Buch von Leonardo da Pisa (später unter seinem Spitznamen Fibonacci bekannt), wird die Kaninchenfrage gestellt, deren Lösung eine tabellarische Zahlenfolge liefert: 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – 55 – 89 – 144 – 233 – 377 – …; ausgehend von den Zahlen 1 und 1 ist jede Folgende die Summe der beiden vorhergehenden Zahlen.

Diese Reihe ist insbesondere durch Johannes Kepler in seiner „Weltharmonik“ von 1619 in Annäherung des Goldenen Schnitts gesetzt und als das schöne Verhältnis, in dem „nun aber die Idee der Zeugung verborgen liegt“, bezeichnet worden.

Auch Le Corbusier nutze die Verhältnisfolge, jedoch mit anderen Ausgangswerten, für die Entwicklung seiner Modulor-Skala.

Und Jay Hambidge in seiner Theorie der Dynamischen Symmetrie bezieht sich auf die Fibonacci-Reihe, deren Abfolge er als wahrnehmbare Flächenverteilung in der Natur auffasst.

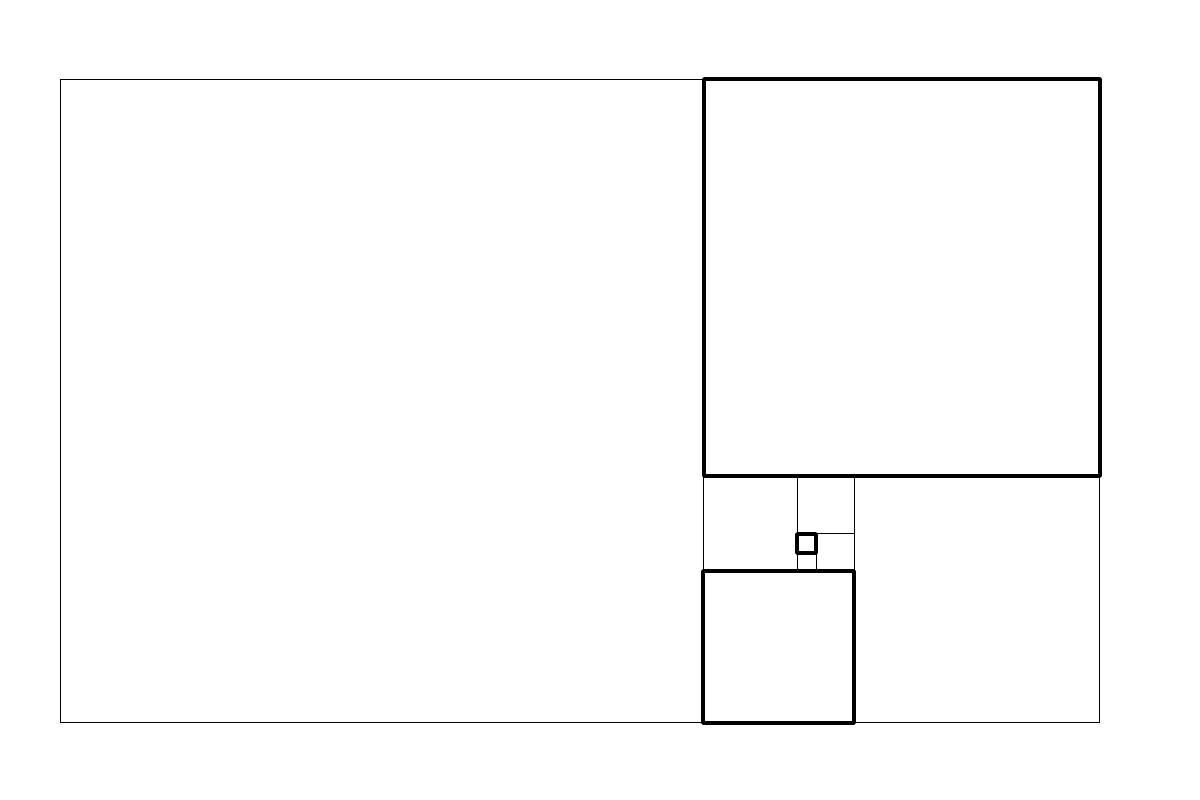
Quadratur der Fibonacci-Zahlen: 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 in spiralförmiger Anordnung

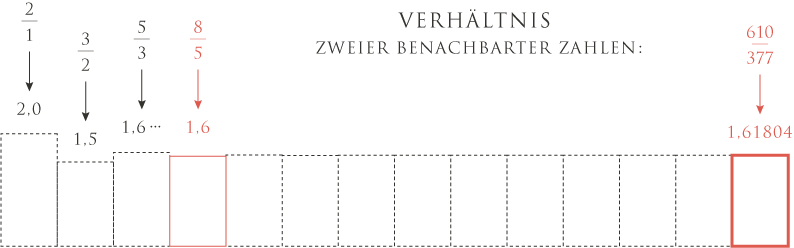
Benachbarte Zahlenwerte

Das Verhältnis benachbarter Zahlen nähert sich dem des Goldenen Schnitts, bereits die Stelle 8 / 5 zeigt die klassische Annäherung zu einem Goldenen Rechteck im Seitenverhältnis von 1,6.