Theorie der Flächenteilung und Ergänzung

Dynamic Symmetry benennt eine Gestaltungstheorie. Sie wurde von Jay Hambidge erarbeitet und 1926 im Studien- und Übungsbuch „The Elements of Dynamic Symmetry“ zusammenfassend veröffentlicht.

Sie geht von einer Verhältnismäßigkeit zwischen einzelnen Teilen aus, wie sie sich im Wachstum von Pflanzen, speziell in der Blattstellung, dem genauen Beobachter zeigt. Die Symmetrie liegt hier in der Entsprechung der Teile untereinander, wie dies etwa in der Fibonacci-Reihe der Fall ist, da jede Zahl als Summe auf ihr vorhergehendes Zahlenpaar verweist. Jay Hambidge nennt solch eine Übereinstimmung in Abgrenzung zur statischen die Dynamische Symmetrie.

Das Beispiel aus der Pflanzenwelt ist dabei eher nur Hinführung zum Thema, ihr Kern ist die Analyse griechischer Kunstwerke, ihr Ziel aber ist das Verständnis bestimmter Rechteckformen mit ihren Unterteilungen. Eine erste Unterteilung, so gesehen das erste Hilfsmittel der Symmetrie, ist mit der Diagonalen gegeben.

Eine zweite Unterteilung ergibt sich aus einer Linie, die zur Diagonalen rechtwinklig verläuft und Reziproke genannt wird bzw. die reziproke Fläche bestimmt. Das dritte wichtige Hilfsmittel ist das Komplement, das Ergänzungsstück, welches ein beliebiges Rechteck zu einem Quadrat ergänzt. Die Verwendung dieser Hilfsmittel zielt im Allgemeinen darauf, Rechtecke als Flächen wahrzunehmen und z.B. Linien innerhalb eines Designs dahingehend zu begreifen. Nach Hambidges Analyse lag genau darin die Kunstfertigkeit der Griechen, Flächen und keine Linien zu entwerfen. Verwendete Flächen standen in einem rationalen Verhältnis zueinander und waren aufeinander abgestimmt. Die bevorzugten Rechteckformen hierfür waren das Quadrat, die Maßverhältnisse der Wurzelzahlen bis √5 sowie das Goldene Rechteck.

Die Dynamische Symmetrie wiederum greift diese Rechteckformen auf, zeigt Teilungs- und Ergänzungsvarianten und gibt Hambidges Unverständnis der Welt, den Künstler nur als bloßes Medium, das blind, unintelligent und auf eine schaffende Sehnsucht reagierend, zu betrachten Übungen zur Besserung.

Diagonale und Gleichheit

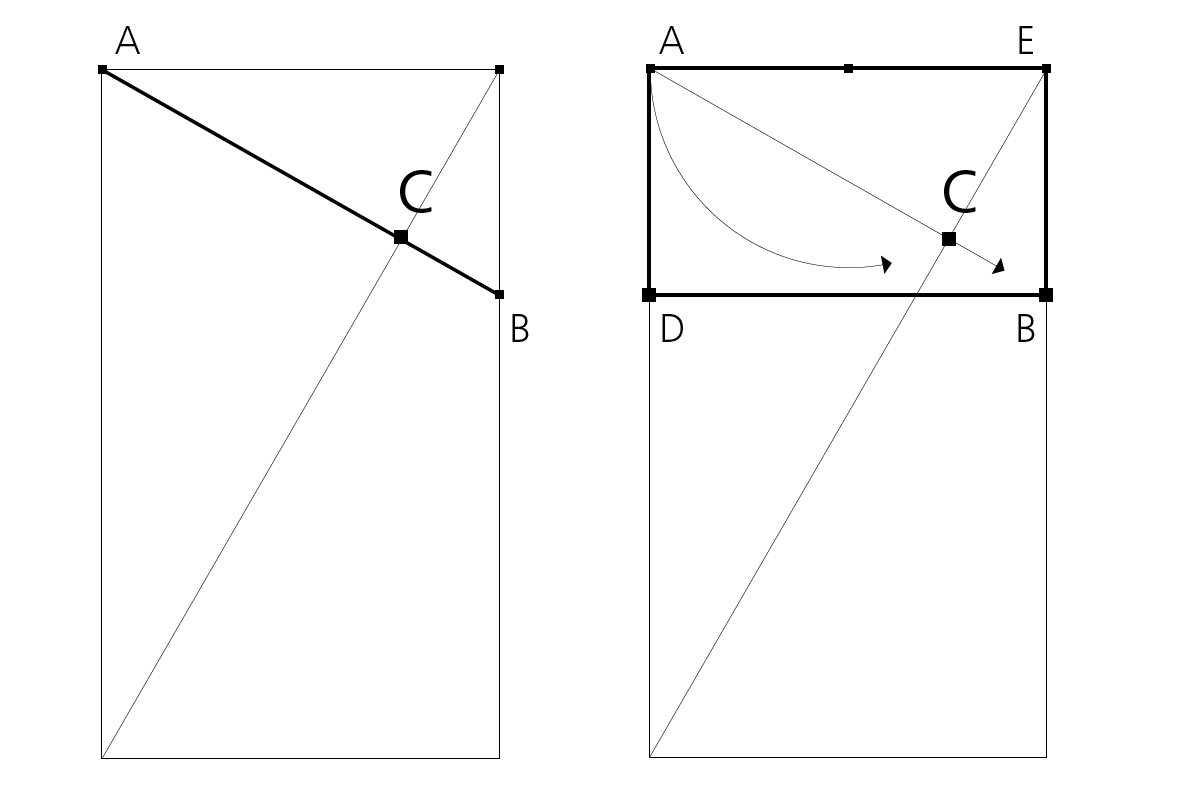
In einem Viereck ist sie eine gerade Linie, die zwei gegenüberliegende Ecken verbindet, so ist die Diagonale seit der Antike definiert. Da jedes Rechteck mit derselben Diagonale gleich ist, sind Vergrößerungen/Verkleinerungen anwendbar, auch in asymmetrischer Konstruktion.

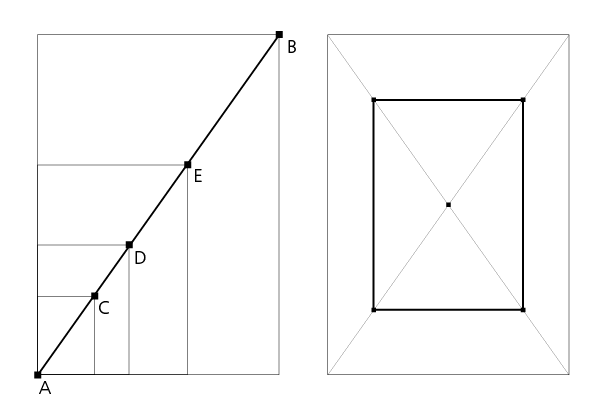
Bild 1: Die Flächen AC, AD, AE sind durch die Diagonale AB zum Rechteck AB gleich.
Bild 2: zentrische Verkleinerung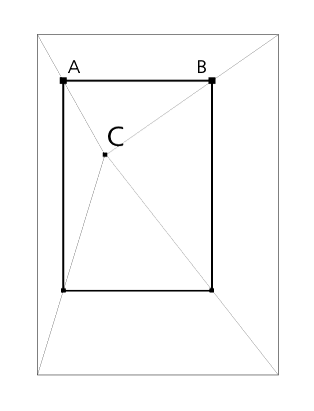
Bild 3: Die Strecke AB ist gegeben, in Punkt C treffen sich die Diagonalen.

Reziproke, Spirale und Teilung

Die Reziproke verläuft rechtwinklig zur Diagonalen innerhalb eines Rechtecks. Sie ist die Diagonale eines kleineren Rechtecks, das wiederum durch eine Reziproke ein weiteres Rechteck erzeugt. Dieses System ergibt eine spiralförmige Anordnung der folgenden Rechtecke. Teilungen sind gegeben, welche die gesuchten Dynamischen Symmetrien sind.

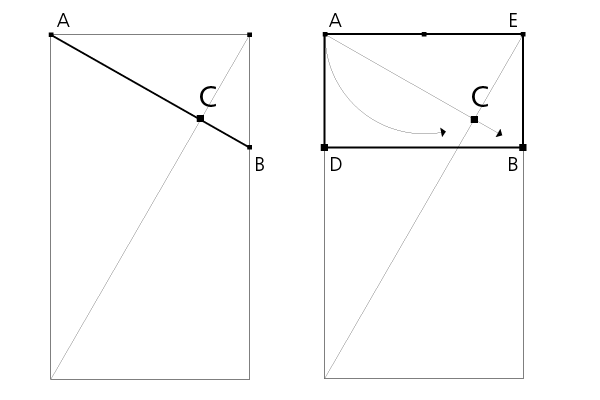
Bild 1: Die Reziproke AB und trifft in Punkt C die Diagonale im rechten Winkel
Bild 2: Konstruktion über den Halbkreis im Durchmesser AE zur Findung von Punkt C. Strecke AC wird zu B verlängert. AEBD ist die reziproke Fläche zum Ausgangsrechteck.

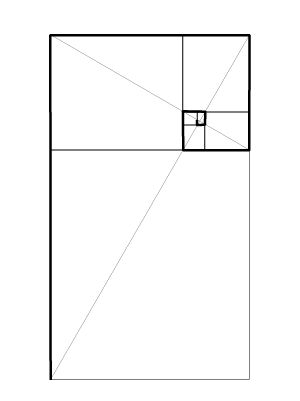
Bild 3: Spirale eines √3-Rechteck

Komplement und Ergänzung

Das Komplement eines Rechtecks ist das Ergänzungsstück zu einem Quadrat. Wie in der Malerei gängig, können Farbwerte durch Einsatz ihrer Komplementärfarbe betont oder neutralisiert werden. Nach Hambidge gilt auch für Rechteckformen die Möglichkeit, Varianten in diesem Sinne zu erzeugen, z.B. Flächenteilungen.

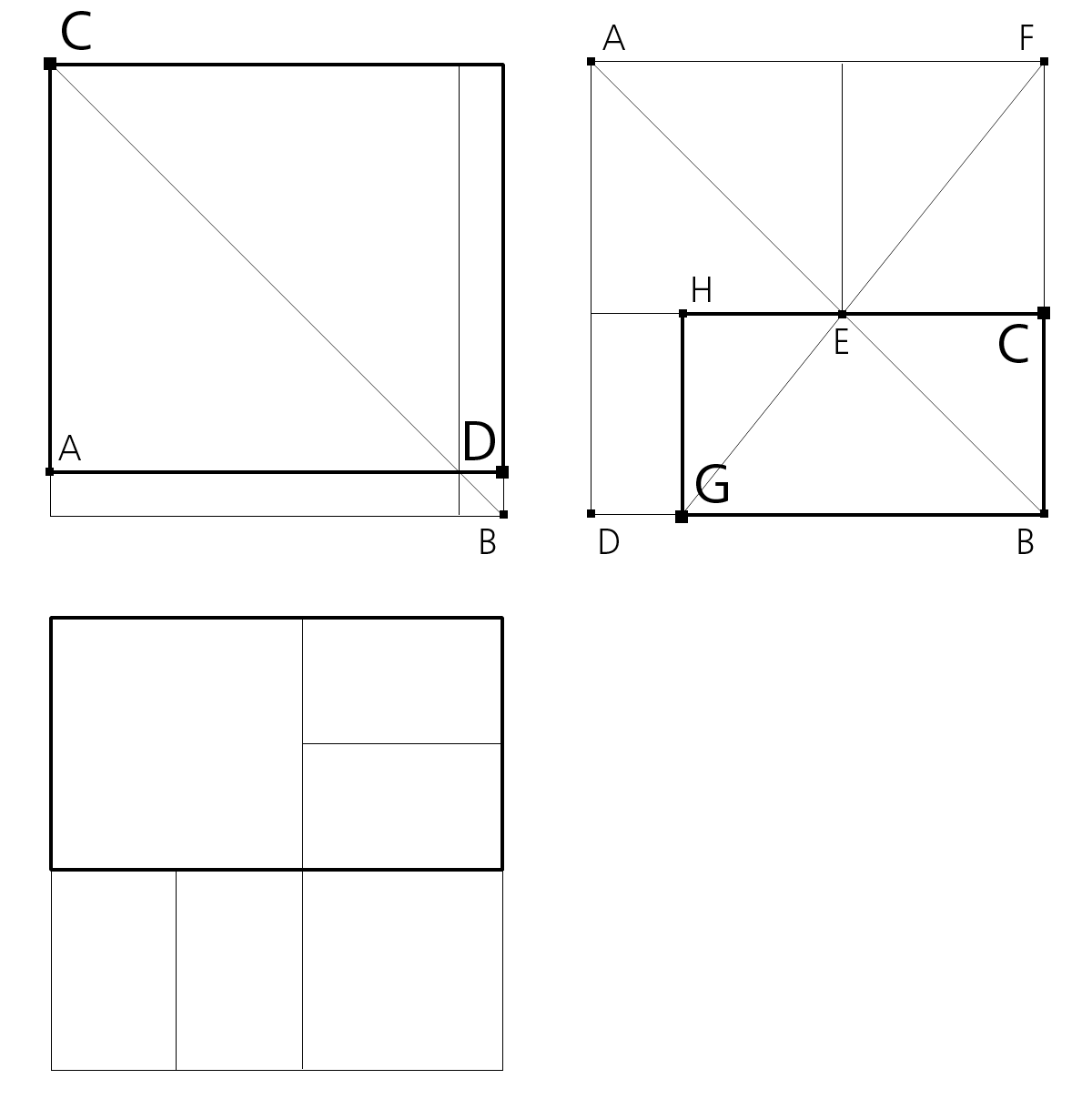
Bild 1: CD ist das Komplement zu AB
Bild 2: Teilungsmuster: DC ist ein √5-Rechteck, GC ist ein 1.809-Rechteck, konstruiert über das Quadrat AE im Komplement AC.
Bild 3: Teilungsmuster mit einem √5-Rechteck unten, zwei Quadraten und 4 Goldenen Rechtecken